IL SUONO IN UNO SPAZIO CHIUSO - PARTE SECONDA

Teoria modale

Concentriamoci prima sulla regione delle basse frequenze dove il campo acustico nello spazio è dominato dalle risonanze dell’ambiente stesso: le frequenze di risonanza di una stanza si possono calcolare secondo l'analisi modale. Trascurando i dettagli matematici, si può considerare la stanza come una guida d'onda chiusa, vale a dire una cavità risonante.

L'onda di pressione acustica viene riflessa dalle pareti e la distribuzione del campo sonoro è la complessa combinazione lineare di modi di propagazione assiali tangenziali ed obliqui: i modi assiali considerano una sola dimensione della stanza, quelli tangenziali coinvolgono due superfici e quelli obliqui tutte e tre. La distribuzione della pressione sonora è fortemente simmetrica e presenta zone a maggiore e minore pressione.

Quando all'onda di pressione sonora proveniente dalla sorgente si sovrappone un’onda che è stata riflessa dalla parete si origina un'interferenza: se l'interferenza è costruttiva il risultato è l’instaurarsi di onde stazionarie all’interno del locale. Di conseguenza la pressione sonora di un tono a quella frequenza di risonanza verrà rinforzato dalla vibrazione dell’aria contenuta all’interno della stanza; gli altri toni, al di fuori delle frequenze di risonanza, vengono attenuati senza ricevere alcun sostegno energetico da parte del comportamento acustico del locale. Le frequenze di risonanza si calcolano in base alle dimensioni geometriche del locale stesso e ad alcuni parametri accessori che assumono valore di numeri interi. Riportiamo a titolo di esempio le frequenze di risonanza per una stanza con dimensioni 5, 4 e 3 metri:

34.30 Hz, 42.88 Hz , 52.91 Hz, 57.17 Hz, 71.46 Hz, 79.26 Hz, 85.75 Hz, 92.36 Hz, 103.06 Hz, 108.62 Hz, 109.81 Hz, 123.80 Hz, 128.63 Hz, 133.12 Hz, 140.76 Hz.

Acustica geometrica

Al di sopra della frequenza di Schroeder le risonanze sono talmente sovrapposte tra loro da non poter più distinguere i singoli contributi di queste al suono complessivo, perciò è necessario sostituire la descrizione del comportamento del suono secondo la teoria modale con un nuovo modello valido anche alle frequenze la cui lunghezza d’onda è trascurabile rispetto alle dimensioni dell’ambiente e degli oggetti presenti in esso. La letteratura suggerisce un approccio di natura geometrica basato sul concetto di raggio sonoro, anziché su quello di onda, che si propaga nello spazio lungo traiettorie rettilinee e che viene riflesso in modo speculare quando incontra un ostacolo.

La riflessione di un raggio sonoro su una superficie rigida è tale che il raggio incidente e quello riflesso si trovano sullo stesso piano e formano angoli uguali con la perpendicolare alla superficie d’incidenza. È lecito pensare al raggio sonoro riflesso come se fosse emesso da una sorgente ipotetica dall'altra parte della superficie: è una sorgente dello stesso segnale in posizione speculare rispetto a quella reale.

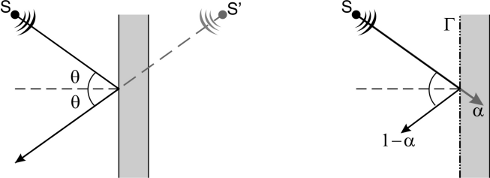
Se l'interfaccia non è perfettamente rigida il raggio riflesso ha un'ampiezza ridotta dal coefficiente di riflessione della superficie, il quale vale 1 se una superficie è totalmente riflettente e 0 per una superficie totalmente assorbente. Il coefficiente di assorbimento acustico dipende dall’angolo d’incidenza e dalla frequenza del suono, variabili che modificano lo spettro di potenza del suono riflesso e che ne riducono l’intensità.

Questi principi dell'acustica geometrica permettono di studiare il comportamento di un raggio sonoro anche all’interno di uno spazio chiuso come ad esempio la stanza di un appartamento: si può considerare ciascuna riflessione come se avvenisse su un'interfaccia di dimensioni infinite a patto che la superficie sia uniforme, ovvero non presenti irregolarità di dimensioni paragonabili a quelle della lunghezza d’onda del suono. Si possono descrivere riflessioni multiple creando una sorgente immagine del second’ordine S'', simmetrica a quella di prim’ordine S' che a sua volta è posta dietro la superficie d’incidenza simmetricamente alla sorgente reale S, e così via fino a che il raggio sonoro non incontra una parete totalmente assorbente o la sua energia si esaurisce.

La figura seguente illustra, in due dimensioni, la dislocazione di alcuni diffusori immagine rispetto ad una stanza rettangolare al centro: evidenzia come un raggio sonoro riflesso coincida con quello diretto diffuso da un ipotetico altoparlante posteriore. Il suono totale percepito nel punto d'ascolto è la somma coerente del contributo diretto e di ciascun diffusore immagine; è lecito formulare una trattazione analitica secondo il modello di canale multi-path.

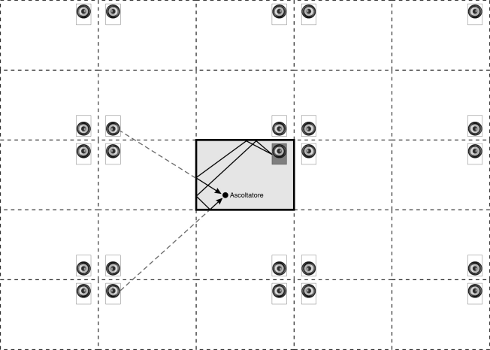
La risposta in ampiezza di un canale multi-path è una funzione fluttuante in frequenza che effettivamente assomiglia alla risposta di una stanza reale.

La descrizione del comportamento acustico dell'ambiente d'ascolto, secondo i criteri dell'acustica geometrica, si complica notevolmente nel caso di stanze la cui geometria non sia rettangolare; a maggior ragione se all'interno della stanza vi sono oggetti ed arredamento che rendono impraticabile l'uso di questa teoria se non attraverso approssimazioni. Tuttavia questo approccio geometrico aiuta a comprendere la natura della distorsione acustica ed è molto utile nello studio della risposta di un ambiente ai fenomeni transitori, sia che si tratti di suoni impulsivi isolati, sia che si tratti delle fasi di transizione che precedono e seguono lo stato stazionario di un suono.