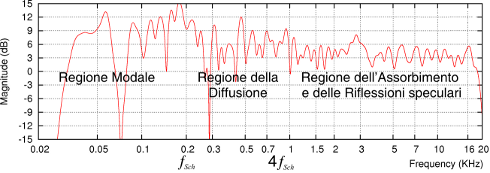
SOUNDS IN CLOSED SPACES FIRST PART

 The acoustic properties of a room dedicated to music listening are determined by many factors such as construction materials of floor and walls, furniture, apertures and in particular by the geometric shape and proportions of the room itself. For acoustic phenomena the useful parameter in assessing room dimensions is the ratio between linear dimensions of the room and the sound wavelength L:

L=Vs / f

Vs (about 343 m/s) is the sound velocity and f is the sound frequency. If we consider audible spectrum, wavelength for 20 Hz is 17 meters, while for 20 kHz it is about 1,7 centimeters. A room can be considered small for low frequencies and very wide for high frequencies. For a closed environment it's necessary to distinguish the low-frequency from the high-frequency description, that is to say it's possible to consider the environment small or wide according to the interesting range of frequencies. Schroeder defined the limit frequency Fsch, different for each environment, which marks the transition from the low-frequency to the high-frequency region. This frequency depends on the ratio between the reverberation time and the volume of the considered room.

So wider and more absorbing rooms, characterized by a short reverberation time, have a lower Fsch, while small, reflecting rooms show this frequency at a higher value. A 54 cubic meters room with 1 second reverberation time has a Fsch = 272 Hz.

So the sound behavior can be studied distinguishing three spectral regions:

1. At low frequencies, under the Schroeder frequency, acoustic behavior is dominated by standing wave presence and the sound pressure level measured in a stationary sinusoidal state varies widely moving into the environment, and so does the frequency response of the room itself. Listening is heavily conditioned by this behavior.

2. The second spectral region, above Fsch, is a transition band covering about 2 octaves.

3. At high frequencies the acoustic behavior is statistical: pressure waves can be approximated as rays, similar to visible light. What we hear in a closed space is the complex superposition of the direct sound from a source and its multiple reflections on the room's surfaces.

Modal Theory

Let's concentrate on the low frequency region where the acoustic field is dominated by the environmental resonances: resonant frequencies of a room can be calculated according to the modal analysis. The room can be considered a closed waveguide, ie. a resonant cavity.

Acoustic pressure wave is reflected by the walls and time distribution of sound field is a complex linear combination of various propagation modes: axial modes consider only one room dimension, obliquous modes all three dimensions. Sound pressure distribution is strongly symmetrical and presents zones with higher and lower pressure.

When the pressure wave coming from the source interferes with wall reflections, this interference causes standing waves to form into the room.

Sound pressure of a tone will be reinforced by the air vibration increasing it against other tones, which are out of the resonance range of the room.

Resonant frequencies can be calculated using the geometric dimensions of the room and accessory parameters that assume integer values.

As an example here are the resonant frequencies for a room with the following dimensions: 5, 4, 3 meters.

34.30 Hz, 42.88 Hz , 52.91 Hz, 57.17 Hz, 71.46 Hz, 79.26 Hz, 85.75 Hz, 92.36 Hz, 103.06 Hz, 108.62 Hz, 109.81 Hz, 123.80 Hz, 128.63 Hz, 133.12 Hz, 140.76 Hz.

Geometric Acoustics

Above Fsch frequency, resonances are so strictly superimposed not to be distinguishable, so it's necessary to change the description we use.

Literature suggests a geometrical approach based on the concept of sound ray rather than wave, propagating into space with rectilinear paths and reflected as in a mirror by obstacles.

Ray reflection on a flat surface is such that the incident ray and the reflected one lie on the same plane and form equal angles with the perpendicular to the incidence surface. We can think to the reflected sound ray as if it was emitted by a virtual (image) source on the other side of the surface: it's a source of the same signal in a mirror position in respect to the real source.

If the interface is not perfectly rigid the reflected ray has a reduced amplitude by the reflection coefficient of the surface, equal to 1 if a surface is perfectly reflecting and to 0 if a surface is perfectly absorbing. Reflection coefficient depends on the incidence angle and sound frequencies, and all these variables modify the spectrum of reflected sound and reduce its amplitude.

These geometric acoustic principles allow to study the behavior of a sound ray even within a closed room: each reflection can be considered as happening on a infinite surface, given the surface uniformity, that is to say absence of irregularities of comparable dimensions to sound wavelength. We can describe multiple reflections creating a second order virtual (image) source S'', symmetrical to the first order S' that in turn is behind the reflection surface in a symmetrical position to the real source S, and so on until the sound ray mets a fully absorbing wall or its energy fades away.

The following figure illustrates, in 2 dimensions, the positioning of some virtual sources in respect to the rectangular room in the figure's center: we can notice the virtual sources positions and the fact that the listener (Ascoltatore) is hearing a sum of the direct sound with all the virtual (image) sources contributions; so we can consider this situation a true multi-path channel.

Amplitude response of a multi-path channel is a frequency fluctuating function that is quite similar to a real room frequency response.

Acoustic behavior of a listening room, according to geometric acoustics, gets very complicated in case of rooms which have a geometry different from rectangular; more so if the room contains furniture and objects: this implies the use of approximations to simplify geometric acoustics approach.

But this approach helps to comprehend the nature of the acoustic distortion and is very useful in the study of the environmental response to transitory phenomena, be those isolated impulses or transitory phases preceding and following a stationary state sound.