SOUND IN CLOSED SPACES SECOND PART

Modal Theory

Let's concentrate on the low-frequency region where acoustic field in space is dominated by environmental resonances: resonant frequencies of a room can be calculated according to modal analysis. Leaving out mathematical details, we can consider the room as a closed waveguide, in other words a resonant cavity.
Acoustic pressure wave is reflected by room walls and the distribution of the sound field is the linear combination of axial, tangential and oblique propagation modes: the axial modes involve only one room dimension, the tangential ones two and the oblique all three.
Sound pressure distribution is strongly symmetrical and presents high and low pressure zones.

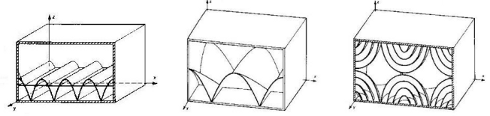
When reflected waves superimpose with direct waves, an interference originates: if interference is constructive the result are standing waves into the space. As a consequence the sound pressure of a tone at a resonant frequency will be reinforced by the room air; other tones, out of resonant ranges will be attenuated witout receiving sustain by the environment.
Resonant frequencies are calculated using geometrical dimensions of the room and some accessory parameters that assume integer values.
As an example here are the resonant frequencies of a room which dimensions are 5, 4 and 3 meters:
34.30 Hz, 42.88 Hz , 52.91 Hz, 57.17 Hz, 71.46 Hz, 79.26 Hz, 85.75 Hz, 92.36 Hz, 103.06 Hz, 108.62 Hz, 109.81 Hz, 123.80 Hz, 128.63 Hz, 133.12 Hz, 140.76 Hz.

Geometrical Acoustics

Above Schroeder  frequency, resonances are so superimposed not to be distinguishable anymore, so it's necessary to change the modal description with a new model which can be used when wavelengths are negligible in respect to environmental dimensions.
Literature suggests a geometrical approach based on the concept of a sound ray instead of a wave, propagating into space along rectilinear paths and is reflected as in a mirror when meeting an obstacle.
Sound ray reflection on a rigid surface is such that incident and reflected ray lie on the same plane and form equal angles with the perpendicular to the incidence surface.
We can think to the reflected sound ray as emitted by a hypothetical source located on the other side of the surface: it's a source of the same signal in a mirror position in respect to the real one.

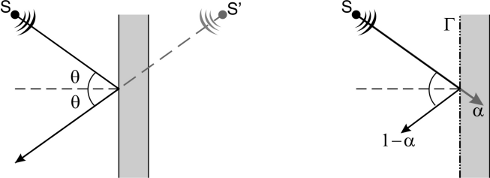
If the interface is not perfectly rigid the reflected ray has a reduced amplitude by the surface reflection coefficient, which equals 1 if a surface is totally reflecting, 0 if a surface is totally absorbing.
Acoustical reflection coefficients depend on the sound frequencies and incident angles, variables which modify the sound spectrum and reduce its intensity.
These geometrical acoustics principles allow us to study the behavior of a sound ray even within a closed space like an apartment room: one can consider every reflection as happening on an infinite surface if said surface is uniform, that is to say it has no irregularities comparable to sound wavelength.
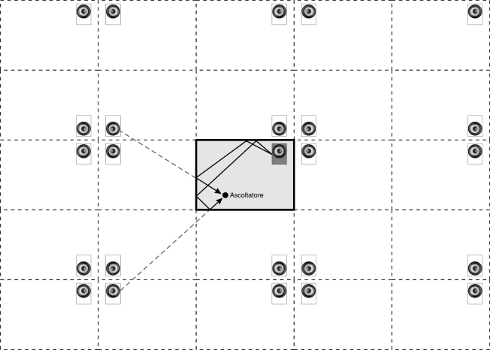
Multiple reflections can be described creating an image source of the second order S'', symmetrical to the first order one S' which is behind the incidence surface and is in turn located symmetrically to the real source S and so on until the sound ray meets a totally absorbing surface or its energy fades completely.
The following figure illustrates, in two dimensions, the dislocation of some image sources in respect to a rectangular room (center): a reflected sound ray is coincident to a hypothetical direct ray diffused by a rear source.
Total sound perceived in the listening spot is the coherent sum of the direct contribution and all the image sources; we can formulate an analysis according to the multi-path channel model.

Amplitude response of a multi-path channel is a frequency-fluctuating function that really approximates the real response of a practical room.
Acoustic behavior description of a listening room according to geometrical acoustics becomes really complicated in case of non-rectangular rooms; more so if the environment contains objects and furniture, rendering impractical the use of this theory if not through approximations.
Anyway this approach helps to understand the nature of acoustical distortion and is very useful when studying the response of an environment to transitory phenomena, be they isolated impulsive sounds or transitional phases preceding and following a sound stationary state.

Tangerinetech Engineering

Simone Bianchi
Owner

http://www.tangerinetech.net/