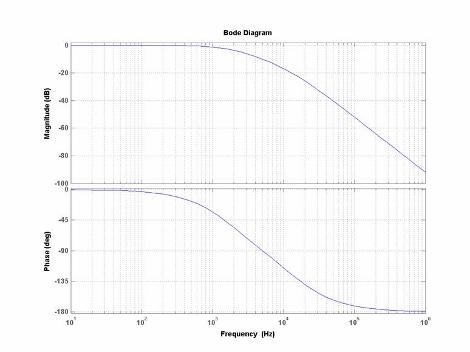
SOUND VELOCITY, RESONANCE AND BOWMAKINGby Simone Bianchi, TangerineTech Engineering http://www.tangerinetech.net 1. Introduction Seeking a scientific approach (or at least a science-inspired one) to musical instrument making, we have to take into consideration some basic physical parameters. Which physical parameters are 'interesting' to be characterized in a musical instrument is no little thing to assess, but some 'educated guessing' can rescue us. Frequency response, for instance (ie what frequencies the instrument will amplify or attenuate, when stimulated by them) is surely an audible parameter, as are the time-decay characteristics of the sound in the long period, possibly due to internal reflections of soundwaves within the instrument's structure. Let's stop for a little on the frequency response, possibly the single most important parameter in sound perception. It is usually represented as a diagram on Cartesian coordinates:
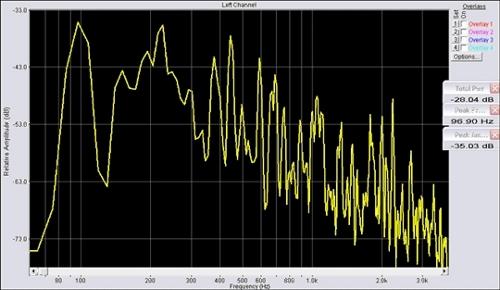
simplifying quite a lot, I'll say the first diagram represents the system's response to frequencies in terms of volume (amplitude) while the second represents response delays (phase). The frequency response of a musical instrument is never linear. That means the stimulus given by the player's bow and fingers won't be amplified by the instrument all the same way. Here is the spectral analysis of a cello (averaged on a whole musical excerpt):
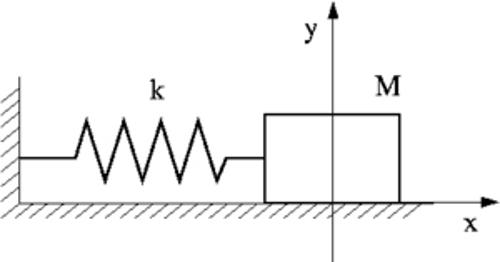
We can observe a response which is considerably non-flat, even though we have to take into consideration the stimulus nature, surely different from a controlled spectrum measurement signal. However an instrument's response, in general, is not flat. This defines the sound and 'character' of the musical instruments themselves. Observing the frequency responses of different instruments, they will vary according to the 'character' of the 'specimen'. Moreover, in the case of bow instruments, the bow itself will have a very important influence on the final result. 2. A simplified model of the bow system / Compression waves Let's focus on the bow stick, which we'll model in a very 'reductive' way:
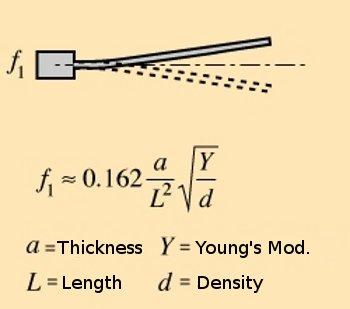
The spring (elastic constant k) represents the wood's elasticity, mass (M) represents inertia of the materials the bow is made with. w = sqr (k/M) w = omega (pulsation) sqr = square root k = spring's elastic constant M= system mass That is to say the frequency (which depends directly from pulsation) at which the system will resonate will be higher as the elastic constant of the wood gets higher, keeping the same system mass, and will be lower as the system mass gets higher, keeping the same wood elastic constant. We'll get back to this in a while; for now let's evaluate the possible influence of the resonance frequency of the bow on the behavior of the whole instrument during a performance. The bow transmits the stimulus given by the musician to the instrument, filtering it according to its mechanical characteristics. The bow's resonance frequency conditions heavily the bow's response to player's stimulus, attenuating the harmonic components which are spectrally far from the central frequency established by the precedent equation. Will there be (and this is left to the luthier to solve!) an optimal bow-system resonance frequency which is ideal to enhance the player-instrument link? Young's modulus Y is defined as: Y = s/e s = applied force / application area e = relative length change It's rather obvious that Young's modulus is directly connected to the wood elastic constant, so it's in direct relation to the resonance frequency of the bow-system. A greater Y value brings a greater k value and a higher resonance frequency. But Y doesn't take into consideration M, mass, and is therefore an insufficient parameter in order to characterize the 'frequency response' of the bow-system. Let's expand the expression to see what other parameters can be added to obtain a more satisfying expression, directly correlated to resonance frequency: Y = (f / A) / (l / L) f = applied force A = area l = length change L = length Since (in abs. value) f /l= k (spring elastic constant) Y = k (L/A) which yields k = (YA)/L. Since w = sqr(k/M) we obtain w = sqr (YA/LM) where: Y = Young's modulus A= surface L = length M = mass. But mass can be expressed referring to density (d) and volume (V). w = sqr (YA/LM) becomes w = sqr (YA/LdV) simplifying: w = sqr (Y/d) * sqr (A/LV) So, resonance pulsation depends on 2 factors: sqr (A/LV) (which depends on physical configuration) and sqr (Y/d). This last factor depends on the intrinsic properties of the material. It's the square root of wood's Young's module divided by its density. In other words, it's the sound velocity in the wood. v(sound) = sqr (Y/d) Finally: w = v(sound) * sqr (A/LV) 3. Simplified model of the bow-system / other oscillations As regarding 'transverse' oscillations it is valid the following relation (omitting the demonstration, valid for thin materials, which gives the first harmonic, the most important one:
Here too we can see a term (0.162 a/L^2) depending on material geometry and another term ( sqr (Y/d)) which is again the sound velocity. v(sound) = sqr (Y/d). 4. Conclusions Under the assumption that the resonance frequency of a musical instrument (and in particular of the instrument's bow) is important in order to determine a musical performance, and this is a truly reasonable assumption, a simple way to correlate this parameter to the wood employed by the builder is to measure the wood sound velocity. This summarizes elasticity and density measurements in a synthetic and elegant way. So the builder will be able to assess the resonant properties of the wood to optimize the performance of the player->bow->instrument 'system'.
http://www.mnt-aq.it/rv/vitale_violoncello.htm https://www.atelierdarcheterie.com http://hyperphysics.phy-astr.gsu.edu/Hbase/music/barres.html
|
   |