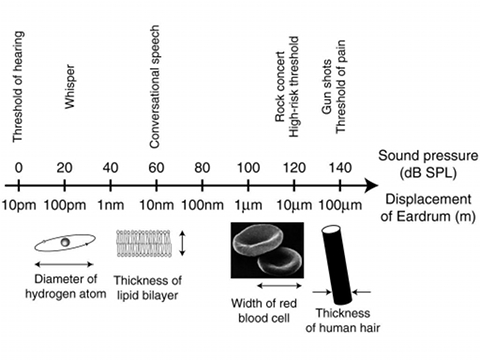
THE DYNAMIC DISTORSIONWelcome again, everybody. Paolo's notes about the Cristiani cello prompted me to reply with some thoughts I'd like to share with you all on this post. The Cristiani is probably one of the most beautiful Strads still in existence, Mendelssohn wrote for it; obviously I immediately obliged the invite to listen it. Dynamic range There was sound everywhere, a feel of fullness never heard before, just as a passing wave. When after some minutes the musician stopped for a while, it was like waking up from a dream. I don't know for what reason, but the musician had brought his own instrument, which at a certain point he played for a while, possibly to focus better on the two instruments' different measurements. I couldn't believe my ears. Leaving out the instrument timbre, not even comparable to the Strad, the most surprising thing was the brisk return to sonic reality. The room at once had become ten times bigger; quite like the difference perceived between a livingroom and a theatre. I had already heard my client's cello, played with the same bow, and in our workshop it seemed to have, in addition to a good timbre, also an important sound impact; that morning it seemed mute! The differences we are speaking of are probably dynamic differences. The following diagram (credit: columbia.edu) will give you an idea of the performances of our auditive system Total dynamic range (difference among the weakest perceived and the most powerful sound which is not painful)is around 130 - 140 dB. Amazing.
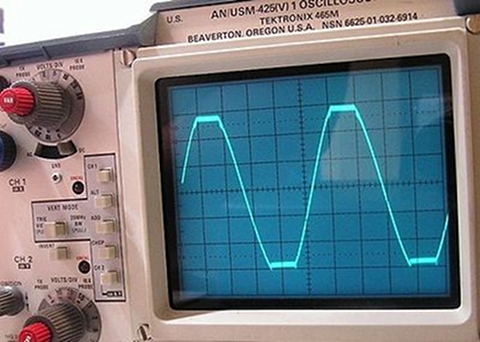
As a comparison, stringed instruments, at a 3 meter distance, can on average reach 95 dB. Some numbers to expand and learn more: http://www.dpamicrophones.com/en/Mic-University/Technology-Guide/acoustical-characteristics.aspx An instrument able to express a greater dynamic range will fill up great spaces with its sound. Compared to it, less endowed instruments will seem toys. I haven't (yet) had the pleasure to meet the Cristiani, but I can bet its dynamic range is greater than the vast majority of its colleagues. In simple words, if you will, this instrument, with the same musician and bow, must be able to sound louder than the others. Much louder. Distorsion Like we were moving in a dream landscape, our audition started, and the sound literally flooded the room. I was paralyzed. There was sound everywhere, a feel of fullness never heard before, just as a passing wave. When after some minutes the musician stopped for a while, it was like waking up from a dream. Distorsion disturbs sound emission and scope, forcing it into the instrument, materializing it. When, like in the ''Cristiani'' case, distorsion is very low, the instrument loses physical presence and becomes just sound. What happens when, for example, a too strong electric signal is passed through an amplifier, exceeding the maximum level the device can manage? The following image (credit: wikipedia.org) gives an example. What should have been a sinusoidal wave is instead distorted assuming angled shapes. The example in figure is called clipping or saturation.
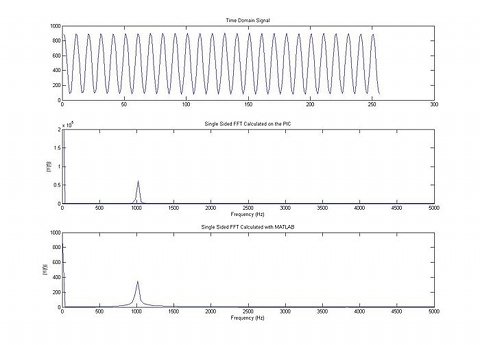
The signal that was provided to the amplifier was pure (sinusoidal), let's say at a frequency of 1000 Hertz, which if analyzed with the Fourier Transform, that is to say decomposed in the frequencies it contained, would have given a representation of this kind: (credit: hades.mech.northwestern.edu):
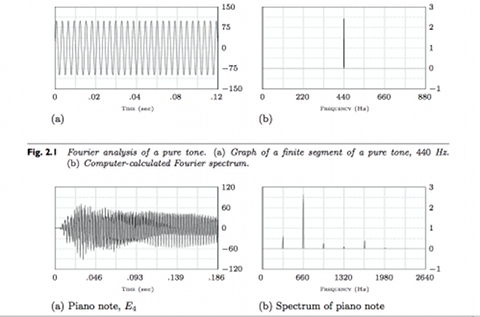
As you can see, a 1000 Hertz pure tone (upper graph) contains the sole 1000 Hertz tone (the peak represented in the two lower diagrams). What happens when a pure 1000 Hertz tone is distorted as you saw in the osciloscope image?
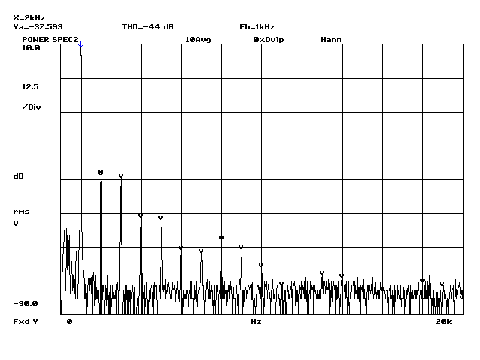
As you can observe, in the output we have the 1000 Hertz signal (fundamental), but also 2000, 3000, 4000, 5000 Hertz signals and beyond, with gradually decreasing levels. These frequencies, not present in the orginal signal, are called distorsion harmonics (or overtones), and they have frequencies which are multiple of the fundamental. Harmonics in music are, we know, what gives the timbre of a note played on a musical instrument: let's look now what happens on the piano:
The upper image shows again the decomposition of a pure tone (electronic oscillator), the lower one the decomposition of a piano note, which contains a fundamental frequency at a 330 Hertz, then others at 660, 990... called harmonics, which have frequencies multiple of the fundamental. http://www.wolframalpha.com/input/?i=musical+note+E4&lk=1 It's a small universe, huh? If in the case of electronic devices we speak about distorsion (the addition of harmonics to the original signal), in the case of a musical instrument harmonics must be present and define its timbre. All in all it's obvious: an amplifier should not have a 'timbre' but just transfer the signal it's amplifying WITHOUT adding harmonics. A musical instrument, on the contrary, uses its harmonics to achieve its timbre. For an electronic amplifier the musical quality is linked to low presence of harmonics, for a musical intrument to the perfect 'dosing' of harmonics. Every instrument has, as in the case of the piano seen before, its distinctive 'cocktail' of harmonics, and obviously every specimen of instrument has its peculiar character. ...When instead, as in the ''Cristiani'' case, distorsion is very low... I think I understand Paolo's statement. In the language of sound reproduction, low distorsion means usually high sound quality. And this is what our cello has: a sound of great quality. It would be nice to measure and 'map' its sound emission for each note played. Maybe one day we will. I couldn't believe my ears It's the destiny often shared by people working with Music. Take care Simone
|
   |